المحاضرة الثالثة في خرائط التوزيعات

د.ولاء على

الأعمدة البيانية:

١.الأعمدة البيانية البسيطة 

٢.الأعمدة البيانية المتجاورة 

٣.الأعمدة البيانية المقسمة ( المركبة)

٤.الأعمدة البيانية المتداخلة: والتي تنقسم إلى جزئين:

١- تداخل كلى و تسمى ( الأعمدة المنطبعه)

٢- تداخل جزئى

٥.الأعمدة البيانية الدائرية

٦.الأعمدة البيانية المجسمة

١.الأعمدة البيانيه البسيطه :

هى من ابسط طرق التمثيل البيانى التى تستخدم للمقارنه بين الكميات لظاهره واحده بشرط أن تكون أرقام هذه الظاهرة متجانسة و من المشكلات التى تقابل رسم الأعمدة البيانيه و هى صعوبة تمثيل بعض القيم القياسيه فى بعض الإحصائيات فقد يكون المدى كبير بين أصغر رقم و اكبر رقم او تكون الأرقام متقاربه بصوره كبيرة و يمكن التغلب على ذلك بكسر المحور الرأسي حتى يتضح التفاوت فى الظاهرة بوضوح.

* يفضل الإ يكسر العمود و المحور أكثر من مرة و ان كسر الأعمدة لا يطبق الإ فى حاله الأعمدة البيانيه البسيطه

* تكسير الأعمدة من اعلى عندما يكون المدى بين أصغر رقم و اكبر رقم كبير وتكسير الأعمدة من اسفل عندما تكون الأرقام متقاربه فى قيمتها و المدى بين أصغر رقم و اكبر رقم صغير

*لحساب المدى = القيمة العظمى (اكبر قيمة) - القيمة الصغرى (اصغر قيمة)

١- تكسير الأعمدة من اعلى:

مثال: يوضح الجدول الآتى قيمة الواردات فى بعض دول العالم عام ١٩٨٢ بالمليار دولار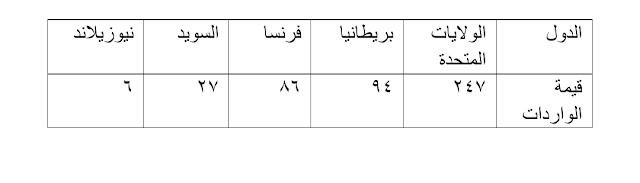

٢- تكسير الأعمدة من اسفل:

مثال : امامك جدول يوضح عدد ساعات إرسال اذاعه الإسكندرية من عام ١٩٧٤ : ١٩٧٩

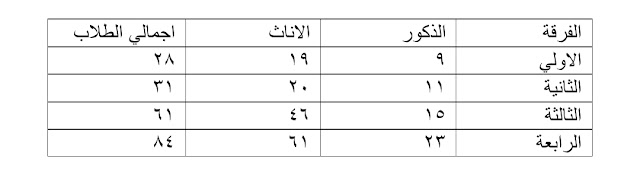
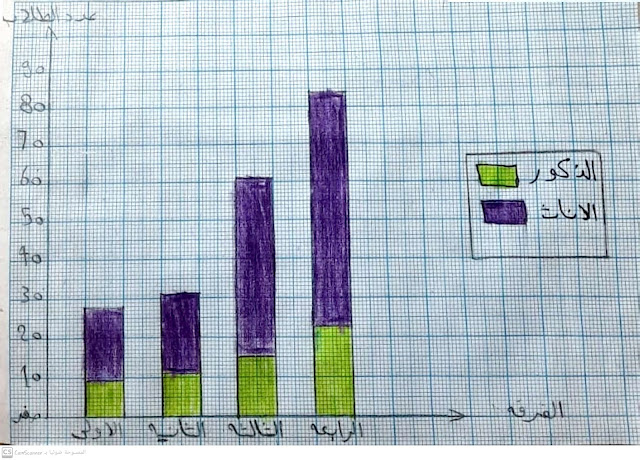
٢.الأعمدة البيانيه المتجاورة:

تستخدم فى توضيح الظاهرة و عناصرها 

مثال : الجدول التالى يوضح عدد الطلاب فى قسم جغرافيا عام ١٩٩٠م

٣.الأعمدة البيانيه المقسمة ( المركبه) :

تستخدم فى توضيح الظاهرة التى تتكون من أكثر من مكون  مثل:

ا.عدد السكان ( الذكور والإناث ) 

ب.مساحه المزروعه حسب موسم ( شتوى ـ صيفي ـ نيلي )

جـ.الحالة التعليمية ( أمى ـ يقرأ و يكتب ـ مؤهل متوسط ـ مؤهلات عالية ) 

د.حسب فئات العمر العرضية ( اقل من ١٥ سنه ـ من ١٥ :٦٤ سنه ـ من ٦٤ فأكثر ) 

في المثال السابق..

٤.لأعمدة البيانيه المتداخلة:

تستخدم لاختصار المساحه الافقيه التى تشغلها الأعمدة و ذلك عندما يراد إظهار المقارنه بين أكثر من ظاهرة خلال فترات زمنية مختلفه و يلاحظ أن العمود الذى يحمل اقل قيمه فى كل ظاهرة او وحده اداريه يكون كاملا من قاعدته و قيمته و جوانبه و تدخل بعد ذلك بقيه الأعمدة الأكثر قيمة.

١- متداخل تداخل كلى:

مثال: الحاله التعليمية لسكان مصر فى عامى  ١٩٦٠ إلى ١٩٧٦ بألف نسمه

٢- متداخل تداخل جزئى:

في المثال السابق..

تعديل المقال